Pérdida de presión en el flujo viscoso a través de una tubería recto
| Δ p = f · l/d · ρ/2 · v2 (Fórmula Darcy-Weisbach) |
| variables con unidades (por ejemplo métrico) | ||
| Δ p | [kg/(m s²) = 10-5 bar = 10-2mbar] | : Pérdida de presión de tubo recto |
| l | [m] | : Longitud |
| d | [m] | : Diámetro Interior |
| ρ | [kg/m³] | : Densidad |
| v | [m/s] | : Velocidad media en el tubo |
| η | [kg/(m s) = Pas] | : Viscosidad Din. |
| ε | [m] | : Rugosidad superficial |
| valores adimensionales | ||
| Re | [-] | : Número de Reynolds Re = ρ v d / η |
| f | [-] | : Coeficiente de Darcy-Weisbach |
Para Re < 2320 (flujo laminar) el Coeficiente de Darcy-Weisbach se calcula según Hagen-Poiseuille:
f = 64 / Re
 Hagen Poiseuille and Couette Flow
Hagen Poiseuille and Couette Flow
Para Re > 2320 (flujo turbulento) el Coeficiente de Darcy-Weisbach se calcula según [Colebrook 1939, página 137]:
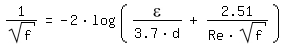
|
Para Re => ∞ (flujo absolutamente turbulento) la ecuación de Colebrook converja a la ecuación de [Prandtl 1933, página 110] según Kármán:
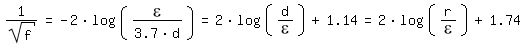
y para ε/d => 0 (tubo liso) a la ecuación de [Prandtl 1933, página 111]:
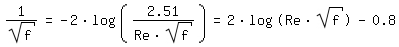
Flujo laminar es posible que Re < 8000 [VDI 1984, página Lb1]. En la zona crítica
de transición (2320 <= Re < 8000) el valor del Coeficiente de Darcy-Weisbach puede ser exagerada
por el medio del cálculo presentada anterior.
El diagrama de Moody [Moody 1944, página 672] es un ilustración con efecto de
las ecuaciones anteriores.
 |
 | |
| Moody Re: 10-106 | Moody Re: 100-108 | |
Con 1/f^0,5 = Re/200 · ε /d y 1/f^0,5 = 2log(r/ε) + 1,74 [Moody 1944, page 676] separa la zona crítica de transición del flujo turbulento.
| Literatura |
| [Colebrook 1939] C.F. Colebrook, Turbulent Flow in Pipes, with particular reference to the Transition Region between the Smooth and Rough Pipe Laws, Journal of The Institution of Civil Engineers, Volume 11, 1939 |
| [Moody 1944] L.F.Moody, Friction Factors of Pipe Flow, Transactions of the ASME, Volume 66, 1944 |
| [Prandtl 1933] L. Prandtl, Neuere Ergebnisse der Turbulenzforschung, Zeitschrift des Vereins Deutscher Ingenieure, Band 77, 1933 |
| [VDI 1984] VDI-Wärmeatlas 4. Auflage 1984 |