Fórmula Darcy-Weisbach
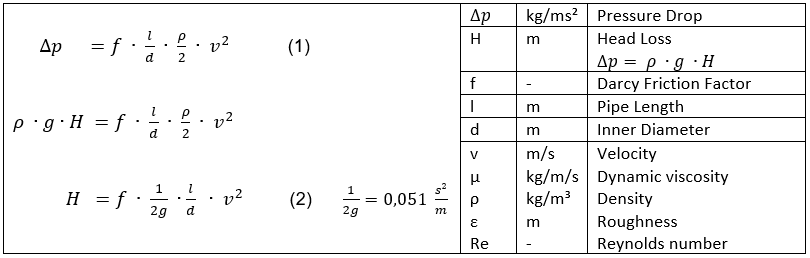 The Darcy-Weisbach equation is an empirical approach for the calculation of pressure losses related to frictional flow in straight open channels and piping.
The analytical approach with a system of differential equations provided by [Navier 1822] can only be integrated for a few particular
cases. Specialized software packages provide iterative solutions. In everyday life of engineers the Darcy-Weisbach equation has
established itself due to easy handling.
Table 1 shows equations of major authors from the first half of the 19th century regarding pressure loss in straight piping.
The empirical equations were derived from experiments with turbulent water flow in iron and cast iron pipes.
The Darcy-Weisbach equation is an empirical approach for the calculation of pressure losses related to frictional flow in straight open channels and piping.
The analytical approach with a system of differential equations provided by [Navier 1822] can only be integrated for a few particular
cases. Specialized software packages provide iterative solutions. In everyday life of engineers the Darcy-Weisbach equation has
established itself due to easy handling.
Table 1 shows equations of major authors from the first half of the 19th century regarding pressure loss in straight piping.
The empirical equations were derived from experiments with turbulent water flow in iron and cast iron pipes.
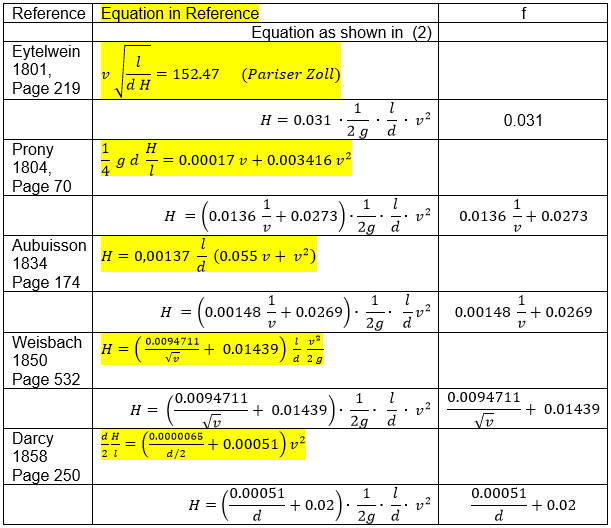 Table 1
[Weisbach 1850, page 529] noted equation (1) as we know it today. Darcy Friction Factors f in Table 1 become dimensionless by the dimensions
of their constants.
The approach of Eytelwein features a constant Darcy Friction Factor.
Weisbach, Prony and Aubuisson show that Dracy Friction Factor f falls in value with rising velocity. Darcy points out that
Friction Factor f falls in value with rising diameters. Both observations are true. The absolute Darcy Friction Factor values
provided by equations of Table 1 match the range of Frictions Factors shown in the Moody diagram. In his equations Colebrook used
dimensionless values for describing the Darcy Friction Factor f (roughness/diameter and Reynolds number).
Table 1
[Weisbach 1850, page 529] noted equation (1) as we know it today. Darcy Friction Factors f in Table 1 become dimensionless by the dimensions
of their constants.
The approach of Eytelwein features a constant Darcy Friction Factor.
Weisbach, Prony and Aubuisson show that Dracy Friction Factor f falls in value with rising velocity. Darcy points out that
Friction Factor f falls in value with rising diameters. Both observations are true. The absolute Darcy Friction Factor values
provided by equations of Table 1 match the range of Frictions Factors shown in the Moody diagram. In his equations Colebrook used
dimensionless values for describing the Darcy Friction Factor f (roughness/diameter and Reynolds number).
 Moody diagram
The work of Navier, Stokes, Hagen, Poiseuille, Reynolds, Karman, Prandtl and Colebrook - to name the most famous - led to the
formulation of the Dracy Friction Factor as we know it today (diagram by Moody). It comprises flow regimes from laminar to completely
turbulent for all Newtonian fluids.
Moody diagram
The work of Navier, Stokes, Hagen, Poiseuille, Reynolds, Karman, Prandtl and Colebrook - to name the most famous - led to the
formulation of the Dracy Friction Factor as we know it today (diagram by Moody). It comprises flow regimes from laminar to completely
turbulent for all Newtonian fluids.
Para Re < 2320 (flujo laminar) el Coeficiente de Darcy-Weisbach se calcula según Hagen-Poiseuille:
f = 64 / Re
 Hagen Poiseuille and Couette Flow
Hagen Poiseuille and Couette Flow
Para Re > 2320 (flujo turbulento) el Coeficiente de Darcy-Weisbach se calcula según [Colebrook 1939, página 137]:
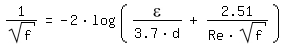
|
Para Re => ∞ (flujo absolutamente turbulento) la ecuación de Colebrook converja a la ecuación de [Prandtl 1933, página 110] según Kármán:
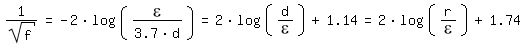
y para ε/d => 0 (tubo liso) a la ecuación de [Prandtl 1933, página 111]:
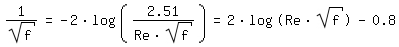
Flujo laminar es posible que Re < 8000 [VDI 1984, página Lb1]. En la zona crítica
de transición (2320 <= Re < 8000) el valor del Coeficiente de Darcy-Weisbach puede ser exagerada
por el medio del cálculo presentada anterior.
El diagrama de Moody [Moody 1944, página 672] es un ilustración con efecto de
las ecuaciones anteriores.
| Literatura |
| [1801 Eytelwein] J.A. Eytelwein, Handbuch der Mechanik fester Körper und der Hydraulik, Berlin bei F.L. Lagarde, 1801 |
| [1804 Prony] R. Prony, Recherches Physico-Mathématiques sur la théorie des eaux courantes, Paris, de L´imprimerie Impériale, 1804 |
| [1822 Navier] M. Navier, Mémoire de l´ Académie des Sciences, Tome 6, 1823, 389 ff |
| [1834 Aubuisson] J.F.Aubuisson de Voisins, Traité D´Hydraulique, Paris, Chez F.G. Levrault, 1834 |
| [1850 Weisbach] J. Weisbach, Lehrbuch der Ingenieur- und Maschinenmechanik, Erster Teil Theoretische Mechanik, 2. Auflage, Braunschweig F. Vieweg und Sohn, 1850 |
| [1858 Darcy] Darcy Mémoire a l´Académie des Sciences, Tome 15, 1858, 141 ff |
| [1883 Osborne Reynolds] Phil. Trans. R. Soc. Lond., 174, 935 ff |
| [1933 Prandtl] L. Prandtl, Neuere Ergebnisse der Turbulenzforschung, Zeitschrift des Vereins Deutscher Ingenieure, Band 77, 1933 |
| [1939 Colebrook] C.F. Colebrook, Turbulent Flow in Pipes, with particular reference to the Transition Region between the Smooth and Rough Pipe Laws, Journal of The Institution of Civil Engineers, Volume 11, 1939 |
| [1944 Moody] L.F.Moody, Friction Factors of Pipe Flow, Transactions of the ASME, Volume 66, 1944 |
| [1984 VDI] VDI-Wärmeatlas 4. Auflage 1984 |