Diámetro hidráulico

Flujo turbulento

El diámetro hidráulico dH debe seleccionarse de tal modo que la pérdida de carga y la velocidad media de flujo sea la misma en tuberías circulares totalmente llenas con dH y en secciones no circulares. El caudal es recalculado:
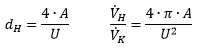		A: sección transversal no circular U: perímetro no circular
canal rectangular:
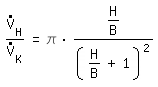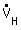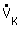		: flujo de volumen en el tubo con dH : flujo de volumen en la sección rectangular H  : altura de canal B  : latitud de canal
H/B 0,2 0,4 0,6 0,8 1 / 0,44 0,64 0,74 0,78 0,79

Flujo laminar

El diámetro hidráulico dH puede determinarse para la sección seleccionada de modo tal que la pérdida de carga y el caudal sean los mismos en tuberías circulares totalmente llenas con dH y en secciones no circulares.
canal rectangular:
dH = H · f (H/B)		H: altura de canal B: latitud de canal, B > H f(H/B): derivación véase más abajo
H/B 0,2 0,4 0,6 0,8 1 f (H/B) 1,96 1,59 1,37 1,22 1,09

Teoría

Flujo turbulento

En caso de flujo turbulento se selecciona el diámetro hidráulico de la tubería de repuesto de modo tal que la tensión de cizallamiento de la pared τ_w y la pérdida de carga Δp de la tubería de requesto sean iguales que la tensión de cizallamiento de la pared y pérdida de carga de un canal no circular. Para ello se considera el equilibrio de fuerzas de la tubería de requesto y el canal no circular:

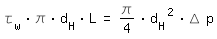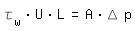		L: Longitud

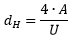Con una velocidad de flujo media igual, se produce la misma caida de presión en una tubería completamente llena con diámetro hidráulico d_H que en una sección no circular. La relación entre la tensión media de cizallamiento de la pared y la velocidad media de flujo es prácticamente igual en ambos sistemas, ya que la distribución de velocidades tiene pocas diferencias en caso de flujos turbulentos.

Los caudales deben ser recalculados con una velocidad de flujo media igual:



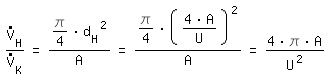
canal rectangular:




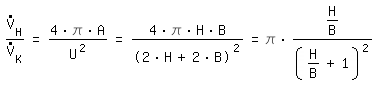
Flujo laminar

En caso de flujo laminar existen, para numerosas secciones, buenas fórmulas de aproximación para el caudal como función de la pérdida de carga. [Berker 1963] resume de forma conjunta soluciones para la distribución de velocidad del flujo laminar en diversas secciones.

Para un canal rectangular con las dimensiones BxH, se cumple con B>H:



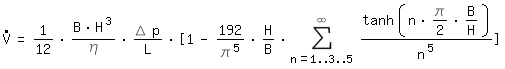
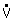: Flujo de volumen     η: Viscosidad Din.      L: longitud de canal


Para B>>H esta ecuación converge frente a la solución para dos planos paralelos, llamada también Flujo de Couette (derivación, véase anexo):




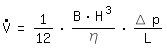
El diámetro hidráulico se obtiene de la siguiente manera:

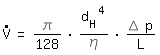		flujo laminar en un tubo (Hagen Poiseuille) (derivación, véase anexo)
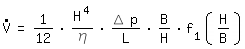		flujo laminar en un canal rectangular

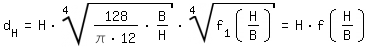
Hagen Poiseuille and Couette Flow

Literatura

[Berker 1963] Tapis Berker, Encyclopedia Of Physics / Handbuch der Physik, Edited by S. Flügge, Springer-Verlag 1963, page 70